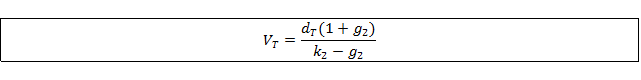6.3 The Dividend Model
John
Williams was one of the first to study mathematically various
models of the intrinsic value of a stock in his now classic 1938
text, “The Theory of Investment Value.”
He credited the definition of intrinsic value to Robert
F. Wiese, “Investing for True Values,” Barron’s, September 8, 1930 p. 5 who
defined the intrinsic value of a stock as:
The proper price of any security,
whether a stock or a bond, is the sum of all future income
payments discounted at the current rate of interest in order to
arrive at the present value.
Williams (1938) refined this to:
Let us define the investment value of
a stock as the present worth of all dividends.
If we write this mathematically, let dt be the dividend to be paid t years from now, and let ke be the discount rate to calculate the present value. Then, the intrinsic value is:
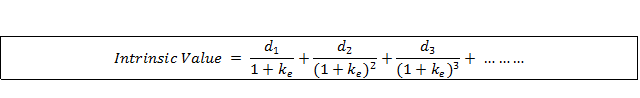
Williams’ contribution was acknowledged by Markowitz, who
developed modern portfolio theory:
“The basic principles of portfolio theory came to me one day
while I was reading John Burr Williams,
The Theory
of
Investment Value.
Williams proposed that the
value of a stock should equal the present value of its future
dividend stream. But clearly dividends are uncertain, so I took
Williams’ recommendation to be to value a stock as the
expected value
of its discounted future dividend stream.”
FOUNDATIONS OF PORTFOLIO THEORY,
Nobel Lecture, December 7, 1990 by
HARRY M. MARKOWITZ
Baruch College, The City University of New York, New York, USA
In
Markowitz’ formulation, we would replace dt in each
equation by E(dt), the expected dividend.
So two
questions arise: how do we forecast dividends, and what is the
discount rate (ke)?
Williams provided two answers.
The simplest was that the current dividend grows at a
constant rate for ever.
This model is sometimes called the constant dividend
growth model or the Gordon growth model (following Gordon 1959).
Another is to assume there are two stages, an “abnormal”
or “short run” stage, and then a “normal” or “long run” stage,
and dividends grow at different rates in the two stages.
The simpler model is
sometimes called the one-stage model (where the first stage
lasts forever). Williams even discussed the application of the
model to non-dividend paying stocks, which we will take up in
the next chapter. For the discount rate, we have to use a risk
adjusted discount rate because future dividends are unknown.
We will say more about this later in the chapter, but we
can now define:
The intrinsic value is the present value
of future dividends discounted at the appropriate risk adjusted
interest rate.
These
two methods of modeling future dividends are the most popular
implementations of the model even today.
However, Williams’ contribution did not stop here.
He identified two major advantages of having a formal
model:
·
It identifies a consistent set of economic assumptions that bound an
assessment of a stock's intrinsic value.
·
You can test the plausibility of the economic assumptions, and also
infer whether market prices are consistent with these
assumptions.
For
example, Williams (page 522) in the section titled “The Degree
of Overvaluation in the 1930 Price” wrote in relation to
American Telephone:
“Even a change in the assumptions so
as to make the company’s period of uninterrupted growth twenty
years instead of ten, which would require it to grow to six and
three quarters its 1929 size, would not have sufficed to give
its stock an investment value in excess of the all-time high of
310 ¼ ex-rights price in 1920.
Twenty years of steady growth would only have warranted a
price rights-on of V0= 300 or a price ex-rights 0f V0
= 283.”
So he
is using the dividend model to argue that the market price of
American Telephone cannot be justified.
In
this chapter, we will describe the two implementations of the
dividend model, and then also look at various ways to forecast
the growth of dividends.
For the discount rate, we will use the Capital Asset
Pricing Model (CAPM).
The CAPM provides an estimate of the risk-adjusted
discount rate for a stock.
The simplest application of William’s theory is the constant dividend growth model. In this model, dt = d*(1+g)t so the current dividend, d, grows for every at rate g. Note that dt is a forecast of the dividend at time t. Mathematically this has a nice implied simplification which can be expressed as follows:
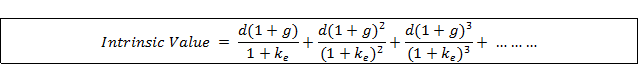
This simplifies to:
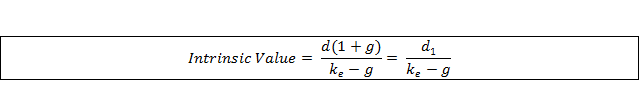
In the two stage model, dividends grow at rage g1 for T years and then grow at rate g2. The dividends are discounted at rate k1 in stage 1 and at rate k2 thereafter. This yields the following formula for the intrinsic value:
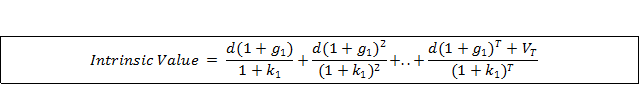
Where