4.4
Portfolio Insurance Problem
Hedging a Portfolio with a Put Option
|
S |
uppose you are managing a stock portfolio, and
want to ensure that its value does not fall below some level, Y, at the end of the next three months. One way to do this is to buy the put option on the portfolio
with strike price (X) which is greater
than or equal to Y and has a maturity
equal to three months.
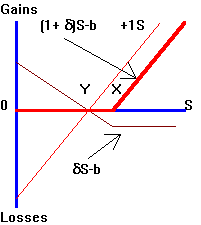
Suppose you choose the strike X such that the gain from the put option (net of its cost) is zero
at Y as depicted in Figure 4.6.
Figure
4.6
Portfolio
Insurance: Put Options
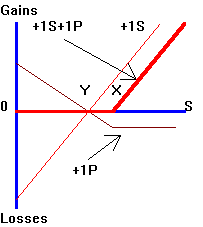
Gains and losses are shown relative to the
target floor Y.
That is, the portfolio of +1S
shows zero gain or loss at Y and gains
(losses) as its value moves above (below) Y. The payoff from a
put option with a strike price equal to X
is depicted by the line labeled +1P.
At S = X,
the put option is "at the money" (i.e., neither in-the-money nor
out-of-the-money), but nevertheless you lose an amount equal to the initial cost
of the put option.
In the online text, the payoff from portfolio +1S+1P
is depicted by the bold red line pointed to by one of the arrows in Figure 4.6.
The floor for this portfolio is at Y
but gains are only realized above X.
This reflects the fact that portfolio insurance is not free.
Given the cost of the insurance, gains relative to Y
must be given up in the interval [Y,X].
In this example, there has been a transfer of risk
from you, the owner of the portfolio, to the writer of the put option.
Hedging Without a Put Option Market
The chances are, of course, that a put option on
your particular stock portfolio is not traded, or is available only for a part
of your portfolio.
If the portfolio value changes according to the
binomial model, however, you can replicate any desired put option by creating a
put option synthetically (i.e., by buying and selling stocks and bonds each
period). In fact, you already know
that we can hold a synthetic put option on the portfolio by holding the delta of
the stock portfolio and b bonds, where
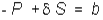
When combined with your original position, this
floor hedge implies that you hold
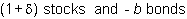
Remember that at each node in the tree, delta will
change and therefore you will need to adjust this position at each node.
For the two-period problem, the tree is as shown in Figure 4.7,
Figure
4.7
Binomial
Tree
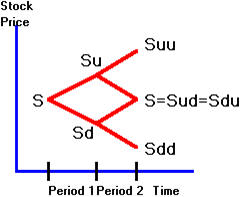
We reproduce the delta at each node as follows:
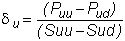
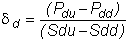
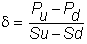
As a result, the initial portfolio of
(1 + d)
stocks and -b bonds must be rebalanced
at the beginning of the second period. The amount of rebalancing necessary will depend on whether
an uptick or a downtick occurs. When extended to the multi-period
binomial model, you have to adjust your portfolio more and more frequently.
If it is costly to trade, as it is in the real world, the transaction
costs can increase significantly.
Without such costs, however, this dynamic hedge
provides the same protection as before, as shown in Figure 4.8.
Figure
4.8
Portfolio
Insurance: Synthetic Put Option
Our analysis assumes perfect markets, and in
particular that the trades implied by delta changes can actually be implemented.
In the 1987 "Black Monday" market crash, portfolio insurance
fell out of favor because the re-trading implied by rapidly changing position
deltas could not be achieved.
Through the binomial option pricing framework, you
have become acquainted with the major insights from modern option pricing
theory. The practical
implementation of this model, however, requires that more periods be added to
the analysis. This is covered in Chapter 5, N-Period Binomial
Option Pricing Model.
 office (412)
9679367
office (412)
9679367