3.7  Two-Period Asian Option Example

You can apply the binomial model to value non-standard options.  The options we will now consider are  Asian options.  The payoff at maturity for an Asian call is max {Sa  - X,0} where Sa  is the average stock price over the life of the option.  This option may be attractive to firms that wish to hedge a stream of transactions over time.  This is because the average price risk becomes a more relevant factor than the price at one time. 

Defining the underlying asset in this way greatly complicates the option valuation problem.  Now, its value depends upon the path followed by the underlying asset, and thus it is a path-dependent option.  Note that the problem is not to determine the option value at the end of its life, but rather at the beginning, when we do not know which path the stock price will take.

The beauty of the binomial approach is that the same principles (i.e., riskless hedge, or synthetic option) still apply and provide a way to calculate the value of the option.  The difference is that the tree diagram becomes more complex.

Consider the tree in Figure 3.12 for the underlying stock price.

Figure 3.12

Binomial Tree for Stock Prices

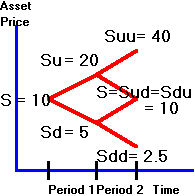
To value an Asian option we first calculate the average stock price at every node.  To simplify this calculation we make the assumption that the average price is calculated only after the first tick is realized (i.e., starting after the end of period 1).  Thus, if there is an uptick in period 1, then Su = 20 but Suu = (20 + 40)/2 where now Su, Suu etc., refer to the average stock price process.

The tree in Figure 3.13 shows you the average prices after making these simplifying assumptions.  We preserve the first part of the tree, and replace the terminal nodes with averages.  Calculated with our simplifications, the average price at the lowest node at the end of period 2 is (5+2.5)/2 = 3.75.

Figure 3.13

Binomial Tree for Average Stock Prices

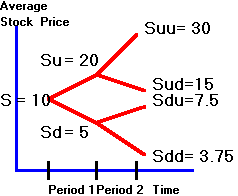
The risk-neutral probabilities remain the same (i.e., 0.34, 0.66 for an uptick and downtick, respectively).  You can now apply the risk-neutral valuation principle as before.  You can verify that the value of the call option is obtained as shown in Figure 3.14.

Figure 3.14

Call Option Value

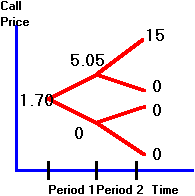
The put option can be valued in the same way.  The tree diagram for the put option is as shown in Figure 3.15.

Figure 3.15

Put Option Value

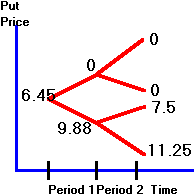
Next, Chapter 4 introduces you to the use of options for controlling risk by applying the principle of dynamic hedging.  An overview of this chapter is provided next in Dynamic Hedging Strategies.