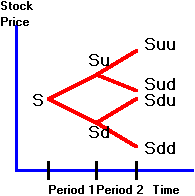
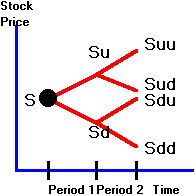
he general two-period binomial model is depicted in Figure 3.1:

Figure 3.1

Two-Period Binomial Tree

The notation we use to develop the general two-period binomial model for European options is:

S  = current stock price;

C  = price of the call option;

X = strike price;

P = price of the put option;

u = uptick in either period;

d = downtick in either period; and

r = 1 plus the (per period) risk-free interest rate

The options will mature at the end of period 2.

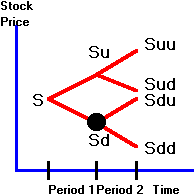
Suppose that at the end of period 1, the stock price moves either up to Su or down to Sd where:

Su = high stock price at the end of period 1 (state H);

Sd = low stock price at the end of period 1 (state L).

In period 2, there are four possible stock values.  Let

Suu = high stock price at the end of period 2, if the stock price is high in period 1;

Sud = low stock price at the end of period 2, if the stock price is high in period 1;

Sdu = high stock price at the end of period 2, if the stock price is low in period 1;

Sdd = low stock price at the end of period 2, if the stock price is low in period 1.

If you are working on the computer, Figure 3.1 is available as a popup window by clicking on Two-Period Tree.  This popup also contains the one-period option pricing model.  You may find it useful to have this popup open while working through this topic.

We start by valuing the call option.  The call is valued recursively by working backwards through the tree.  We start at the end; you know that the value of the call option at the end is one of

Cuu   = max { 0, Suu - X }

Cud   = max { 0, Sud - X }

Cdu   = max { 0, Sdu - X }

Cdd   = max { 0, Sdd - X }

(We assume that Suu > X ; otherwise the option never has any value.)

Now, move back one period.  Suppose we are at Su (i.e., the first tick was an uptick).  At this point, we have only one period left, so we know from Chapter 2 how to calculate Cu.  Similarly, we know how to calculate Cd.  Now, come back to the beginning, where we want to calculate C.  Here, we simply have a one-period binomial model again, where the call value on the uptick is Cu and that on a downtick is Cd.

We will repeat these steps in detail below.  The key step is simply that by working backward, we reduce the two-period problem to a sequence of one-period problems.  At each point, we apply the one-period model (see topic 2.4, Call Option Valuation: A Riskless Hedge Approach developed in Chapter 2).

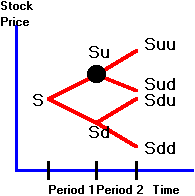
The detailed calculations are as follows. Let Cu be the value of the call option at the node shown by a black circle on the tree in Figure 3.2 and let ku be the hedge ratio.  At this node, we had an uptick in the first period.

Figure 3.2

Position in Tree After an Uptick

In the one-period problem we solved for the value of the call option at the beginning of period 1, C, as:

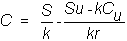
All we have to do to this is substitute Su for S, Suu for Su and so on, resulting in:

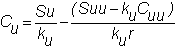
 where

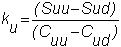
Similarly, you can calculate the value of the call option at the realized downtick node marked in black in Figure 3.3.

Figure 3.3

Position in Tree After a Downtick

By applying the one-period model to this node, we get:

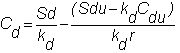
where

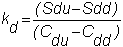
Finally, we come to the first node, the black circle in Figure 3.4.

Figure 3.4

The First Node

Here, we can directly apply the formula from the one-period model:

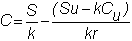
where

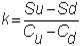
You can see that there is only one difference between how we approached the two-period problem and how we approached the one-period problem.  In the one-period problem, we calculated Cu and Cd from the terminal value of the option contract (i.e., the max conditions).  In the two-period problem, we could use this information only at the end of period 2.  As a result, we first had to calculate Cu and Cd from the period 2 terminal value information using the one-period option pricing model.  We could then use these values for Cu and Cd (in place of the terminal values used in the one-period model) and then repeat the application of the one-period model.

You may want to calculate the general form of the European put option pricing model as an exercise.  Or, you can derive this simply by applying the Put-Call Parity Relationship (See Chapter 2, topic 2.9), at each node.  That is, if you know the value of a European option and the stock price at each node, then the value of the European put option is:

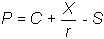
The two-period model is easy to extend to any number of periods.  It can also be used to handle very complex option pricing problems.  For example, it is not necessary that  u and d be constant over time, or that the risk-free interest rate be constant (as long as it is deterministic).  A formal treatment of the multi-period binomial analysis is provided in Chapter 5,  the N-Period Binomial Option Pricing Model.

Next, we introduce options that you can exercise at any time before maturity.  Such options are called American options.  You can  work through the American option problem in the next topic, American Call Option:  Zero-Dividend Case.