2.5
PUT OPTION VALUATION: A RISKLESS
HEDGE APPROACH
Consider
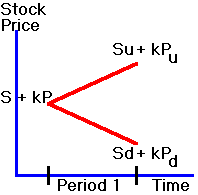
a portfolio of +1 stock and +k puts. The
future payoffs for this portfolio are shown in Figure 2.5.
Figure 2.5
Future Payoffs
The
Hedge Ratio (k)
For
a portfolio to be riskless, you have to choose k
so that the payoff in both states is equal, whether the stock moves up or down.
![]()
This
requires
![]()
which
is called the hedge ratio.
The
Riskless Hedged Portfolio: Put
Options
The
portfolio in Figure 2.5 is known as the riskless hedged portfolio.
It is constructed from the hedge ratio k,
so that for every stock held long k
put options are bought. The
riskless (put option) portfolio is:
S + kP
This
is a riskless hedge because when the terminal stock value is low, the put is
valuable. The converse is true for
a high terminal value. Setting k
equal to the hedge ratio balances the losses with the gains.
The
Cost of the Riskless Hedge
The
cost of acquiring this portfolio today is
S + kP. Since
![]()
the
portfolio end-of-period payoff is a certain amount.
Thus, using the risk-free interest rate, you can equate the cost of
acquisition today to the present value of the certain end-of-period payoff. The end-of-period payoff can be defined by either the up- or
downtick, because both are the same. Let
this be fixed as the realized downtick value:
![]()
By
substituting for k, you can solve for
the value of the put option P.
![]()
This
gives you the price of the put option as a function of the current stock price,
the future stock values, the strike price, and the risk-free interest rate.
For
example, when X = 30, Su = 40, Sd = 20, and
one plus risk-free interest rate r =
1,
![]()
this
gives S +2P = 40 so P
= (40-S)/2,
An
alternative approach to the European option valuation problem is to create a
synthetic call option by constructing an appropriate portfolio consisting of the
stock and the bond. You can see
this approach in the next topic, Option
Valuation: A Synthetic Option
Approach.
 office (412)
9679367
office (412)
9679367