12.5 Application: Options on Futures
|
F |
rom
the Lemma the excess drift rate divided by the volatility is equal for the
future and the call option. This
means that again we merely have to simplify the equation
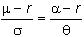
We start with the
assumed futures price process:
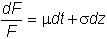
Assume that the value of
the call option is C(F,t), and
applying Ito’s lemma to C,
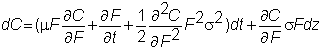
Recall that the drift
rate of the call is (1/C) times the
term multiplying dt, and therefore the
drift rate of C is
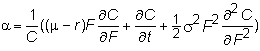
and
the volatility is
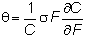
Following the general
method for valuing options, we can equalize the volatility-adjusted drift rate
on the stock and on the call option:
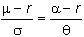
Substituting
for a
and q, we get
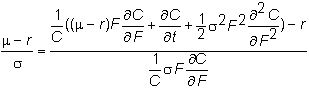
Now,
cancel the s
in both denominators, multiply the right hand side through by C,
and multiply out the denominators to get
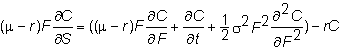
Finally,
cancel the (m-r)
term on either side to get
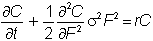
The solution to this
equation is Black’s model.
In Chapter 13, Valuation
Examples and Techniques, you will see how option pricing theory is applied
to real world problems.
 office (412)
9679367
office (412)
9679367