CHAPTER 12: A Unified Approach to Option Pricing
12.1
Equality of Volatility-Adjusted Drifts
|
I |
n this topic, we present
a general method for valuing options which is particularly useful for valuing
options on currencies and on futures, but also applies to common stock.
The method relies on the fact that if two assets are defined on the same
source of uncertainty, then no arbitrage implies that their
“volatility-adjusted excess drift” must be the same.
(Some expositions call this the market price of risk; we refrain from
doing so because it confuses the drift rate with the expected return.)
The general principle is
expressed in the following lemma, due to Garman (1976).
Lemma:
Let f
and g be given by df = mfdt + sfdz
and dg = ngdt + rgdz.
If r is the instantaneous
risk-free interest rate, then
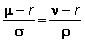
We will show you why
this provides a powerful method for valuing options after we show you the proof.
To prove the lemma, we
1.
construct a riskless portfolio using the two assets, and
2.
use the fact that this portfolio must yield the risk-free return.
For
Step 1, consider the portfolio in which you are long a = (gr) units of f
and short b = (fs) of g.
The value of this portfolio is

The
change in the portfolio over an instant of time is given by
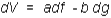
Now,
substitute for df and dg,
and also for a and b, to get
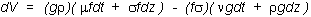
Now,
look at the two terms involving dz.
They are (gr)(sf)dz and -(fs)(rg)dz,
which cancel. Therefore, dV depends only on time, and is risk-free:
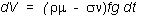
We
now use the fact that this portfolio must yield the risk-free return.
In other words,
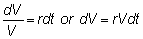
Substitute
for dV and for V = af - bg to get:
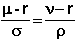
You
can see why we call each term the “volatility-adjusted excess drift.”
For
the remaining part of this chapter we will apply this lemma to option valuation
problems. In the topic Application:
Stock Options you will see how the basic Black-Scholes partial differential
equation is derived, followed by applications to both currency
options and options on futures.
 office (412)
9679367
office (412)
9679367