10.4 Currency Options: Hedge
Parameters
|
|
urrency options are
important instruments for managing exchange rate risk.
As a currency trader, you are interested in knowing:
1.
how your position is exposed to changes in exchange rates, changes in
interest rates for both the strike and the deliverable currency, and changes in
exchange rate volatility;
2.
how you can hedge your position against these sources of risk.
The hedge parameters
provide the answers to 1., and using these parameters traders can identify the
appropriate option trading strategy to answer 2. Online, you can graph the hedge parameters as a function of
any of the underlying variables. The
mathematics underlying these graphs is summarized here; it is the same as for
the continuous dividend yield model, except that rd
replaces the dividend yield.
The call option pricing
formula is
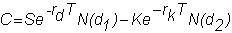
and since
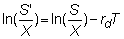
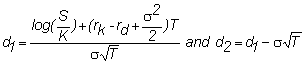
The variables that
affect the option price are
S =
exchange rate
K =
the strike price
s =
the volatility of S
T
= the time to maturity
=
the risk-free interest rate in the strike country
rd
= the risk-free interest rate in the deliverable country
By calculating the
derivative of the call price with respect to each variable, we obtain the hedge
parameters. You may want to compare
these to Comparative Statics, in Chapter 9,
topic 9.3.
Delta
For a call option and a
put option, respectively, delta is given by:
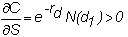
and
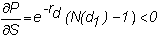
The delta of the call
tells you how the value of the call changes if there is a small change in the exchange rate S.
For example, if you have
written 1,000 currency call options that have a delta of 0.85, then you need to
be long 850 units (= 0.85*1,000) of the bond in the deliverable currency to
create a delta-neutral position. If
delta changes to 0.86, to remain delta-neutral,
you would have to buy an additional 10 units (= (0.86-0.85)*1,000) of the
bond.
You should observe that
because maintaining the hedge requires that you hold the zero-coupon bond in the
deliverable currency, you are earning a continuously compounded riskless rate of
interest equal to rd.
The mathematical details associated with forming a riskless hedged
portfolio are provided in Chapter 12, topic 12.4, Application: Currency
Options.
Gamma
The gamma of a currency
option measures how the delta changes with S.
This provides useful insight into the potential frequency of rebalancing
that is required to maintain some target delta.
That is, the gamma tells you how far you are from some target hedge. For
either a call or a put option, gamma is
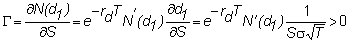
Online, you can see that
a position is most sensitive to changes in delta when it is at-the-money.
Rho
Rho measures the change
in the call option with respect to a change in the riskless interest rate.
For currency options, this is sometimes called the interest rate delta.
There are two rhos, one with respect to the strike country's interest
rate, and the other with respect to the deliverable country's interest rate.
For the strike currency:
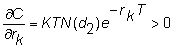
and for the deliverable
currency's risk-free interest rate:
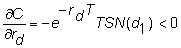
Vega (Lambda or Kappa)
The vega measures the
effect of a change in the volatility of the exchange rate.
It is given by
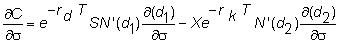
and thus,
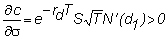
In Chapter 11 you will
see the Black-Scholes option pricing model extended to value options on futures
in topic 11.3, Pricing of Options on Futures.
 office (412)
9679367
office (412)
9679367