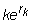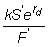10.2 Interest Rate Parity Relationship
Introduction
|
A |
s a prelude to valuing
currency options, we show you an arbitrage relationship that must hold between
spot and forward exchange rates. This
will help you understand how a riskless hedged portfolio is constructed, by
identifying the various opportunity costs involved in dealing with currencies.
In a forward
contract, two parties enter into an agreement to exchange one asset for
another. Unlike an option, the exchange must be carried out.
The price is specified now, as is the date at which the transaction will
occur. This type of contract is
very popular for currency transactions. The
price that is set now is called the forward
exchange rate. This rate will
govern the future exchange, no matter what the spot exchange rate is in the
future.
The existence of a
forward exchange market enables the construction of a riskless portfolio.
As you will see, this implies that certain relationships must hold among
the spot exchange rate, the forward exchange rate, and interest rates in the two
countries.
These relationships are
summarized by the interest rate parity theorem. This theorem also tells you how to value a forward contract.
We start with some
notation. Understanding the
notation is particularly important when dealing with currencies. To maintain consistency (particularly when we come to
options), we adopt a convention for referencing a country's currency relative to
the option contract: One country's currency is labeled the "strike
currency." The other country's currency is labeled the "deliverable
currency."
Notation:
F
= the forward exchange rate. This
is the number of units of the strike currency to be exchanged for one unit of
the deliverable currency. We set
the maturity of the forward contract to be one period.
S
= the spot exchange rate. This
is the number of units of the strike currency that can be exchanged
for one unit of deliverable currency at the present time.
F'
and S' are the same as F
and S, with strike and deliverable currency interchanged.
rd
= one-period continuously compounded risk-free rate for the deliverable
currency.
rk = one-period continuously
compounded risk-free rate for the strike currency.
Interest Rate Parity Theorem
Suppose you have k
units of the strike currency to invest for one period.
You are interested in the
final value of the strike currency. If
you consider only risk-free investments, there are two ways in which you could
invest the money.
1.
At the strike currency's risk-free rate.
2. At the deliverable
currency's risk-free rate, where you go through three steps:
a.
Convert k at the spot exchange rate into the deliverable currency.
This gives you kS' of
the deliverable currency. (Recall that S' is the number of units of the
deliverable currency per unit of the strike currency.)
b.
Invest at the risk-free rate in the deliverable currency.
At the end of the
period, you have
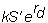
of the deliverable
currency.
c.
Eliminate all risk by entering into a forward agreement to buy back the
strike currency at the forward exchange rate.
This nets you the result
in b) divided by F' (which again is in
the same units as S').
The payoffs from the
first and second strategies are:
Table 10.1
Risk-Free Investments: Two
Strategies
|
Strategies |
| ||
|
|
1 |
2 |
|
|
Time
0 |
-k |
-k |
|
|
Time
1 |
|
|
|
Neither strategy entails
any risk. Therefore, the
two strategies must have the same future (or present) values.
This implies
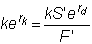
Rearrangement gives us
the interest rate parity theorem:
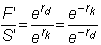
Alternatively, observe
that:
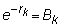
price of a one-period
pure discount bond with face value 1, and, similarly,
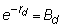
Again, substituting and
rearranging yields:

If the period length is
some number T, the parity
relationship is:
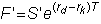
In terms of the strike
currency, the relationship is
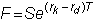
The parity relationship
says that spot and forward
exchange rates should be such that a trader cannot engage in profitable
arbitrage. That is, a
currency trader should not be able to borrow cash in one country,
convert it at the spot exchange rate, invest in the second country, and
at the same time enter into a (zero cash outlay) forward agreement to
cover the future value of the loans, and have some positive amount of
cash left over!
Now that you are acquainted with this important relationship, you are ready to move on to the Currency Option Pricing Model.
 office (412)
9679367
office (412)
9679367