11.3 Pricing of Options on Futures
|
|
ptions on futures have
grown greatly in importance, and are traded on a wide range of underlying
securities. These include interest
rates, commodities, stock indices, and currencies. Some markets in which these instruments are traded include:
Interest Rates:
the Chicago Board of Trade and the International Monetary Market.
Commodities:
the Chicago Board of Trade, the Kansas City Board of Trade, the Commodity
Exchange Inc. (COMEX), the Minneapolis Grain Exchange, the New York Cotton
Exchange, the New York Mercantile Exchange, and the MidAmerica Commodity
Exchange.
Stock Indices:
the New York Futures Exchange and the Index and Option Market (IOM).
Currencies:
the International Monetary Market.
The key difference
between a futures (or forward) contract and other assets is that at the time of
entering into a futures contract, no cash is exchanged.
This means that you must be careful to take this into account when
constructing a hedged portfolio that involves a futures contract.
Assume that the futures
price equals the forward price. You
can recall for the case of an option defined on a stock, (see Interpretation of the Black-Scholes Model in Chapter 6, topic 6.5),
the riskless hedged portfolio consists of short one call option and long
"delta" stocks, expressed as follows:
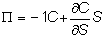
For a futures contract,
the riskless hedged portfolio is constructed from the futures and the option on
the futures contract. However,
this can be related to a riskless hedged portfolio consisting of a stock and an
option by recalling (from Chapter 10) that the futures price equals:
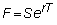
or by rearranging this
equals:
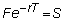
That is, the valuation
of an option on a future is formally equivalent to the valuation problem for an
option on a continuous dividend paying stock.
This problem was solved in Chapter 9, the Continuous
Dividend Yield Model. The only
difference is that we replace the stock price by the futures price, and the
dividend yield is the risk-free interest rate.
This results in Black's
valuation model for options on futures:
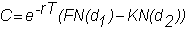
(here, K
is the strike price)
.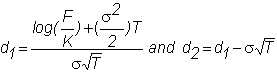
Similarly, the European
currency put option price is either obtained indirectly from put-call parity or
expressed directly as:
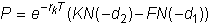
where d1
and d2
are as before.
Example
Consider an option on the S&P500 futures contract.
The current futures price is $460, and the time to expiration is 0.25
years (or 3 months). The strike price is 460, and the three-month risk-free
interest rate is 5%. If the
volatility of the futures price is 20% annually, then the price of the European
put option is $18.10, and equals the price of the European call option.
The appropriate
comparative statics are derived by substituting r for q in
Comparative Statics, topic 9.3 in
Chapter 9.
 office (412)
9679367
office (412)
9679367