![]() 8.2 Single-Index Model
8.2 Single-Index Model
The major assumption of Sharpe's single-index model is that all the covariation of security returns can be explained by a single factor. This factor is called the index, hence the name "single-index model." One version of the model, called the market model, uses a market index such as the S&P500 as the factor, although in principle, any factor that influences security returns can serve as the index. Here, we will adopt the terminology associated with the market model.
Let ri be the return on stock i, and let r
i be the return on the index. The single-index model assumes that we can write![]()
Here,
e is the idiosyncratic or residual or firm-specific return, which means that it is the part not explained by the index. Formally, the single-index model assumes a one-factor return-generating process. In such a process, the variability of all stock returns can be completely described by one common index plus firm-specific events. Individual responsiveness to the index is captured by the weight b1 .The second assumption of the single-index model is that the idiosyncratic returns are independent across firms. This means that the covariance of
ei and ej is zero, and is based on the assumption that the part of the return that is not explained by the index results from purely firm-specific events.This independence leads to a significant simplification of the covariance matrix of returns. In particular, the off-diagonal terms in the matrix take on a simple form. Recall, that the covariance between the returns of i and j is
![]()
If you substitute the equation
![]()
multiply ri and rj, and take expectations, you will find that
![]()
Similarly, the variance of ri reduces to:
![]()
As you can see, the variance is the sum of two components. The first is the variance arising from the index, which is called the systematic risk. The second is the firm-specific or unsystematic risk.
Since it is assumed that the unsystematic components are independent across firms, the expression for the portfolio variance reduces to
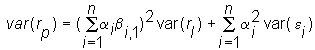
The portfolio problem then simplifies to
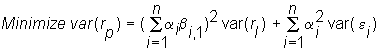
subject to the weights summing to one, and resulting in a desired expected return.
It is instructive to compare the above expression for portfolio variance with the objective function used in the full Markowitz problem:
![]()
where the
a's are the weights of individual securities in the portfolio.You can see that there is a considerable saving in the number of terms contained in the single-index model compared to the full Markowitz formulation. For example, with 100 stocks, the Markowitz problem has 10,000 (100x100) variances and covariances (of which only 5050 are distinct because the covariance matrix is symmetric). This compares to 100 betas, 100 residual variances, and 1 variance of the index in the single-index model.
Most of this simplification comes from the assumption that the unsystematic components are independent, in which case the covariance of returns is:
![]()
This means that the covariance matrix in the single-index model has the security variance terms down the diagonal and the product of the beta and the variance of the index in the off-diagonal part.
There is a close relationship between the single-index model and the CAPM. To see this, recall that the CAPM implies
![]()
where rM is the return on the market portfolio (see the two-fund theorem in Chapter 7). The market portfolio is more appropriately called the tangency portfolio, since it is the point of tangency between the minimum variance frontier and the capital market line.
If we take the expectation of ri in the single-index model and substitute
![]()
we get
![]()
This is the same functional form as in the CAPM, and if the index equals the market portfolio, the result is exactly the same.
On a cautionary note, you should remember first, that the market portfolio in the CAPM is not the same as a "market index." In fact, if you use a market index such as the S&P 500 in the single-index model, it is quite unlikely that it will coincide with the tangency portfolio identified by the CAPM. This will become readily apparent when you use the single-index model to analyze real-world data. Second, you should remember that even though the functional form for the expected return is similar, the single-index model leads to a simplification of the portfolio choice model because of the additional assumption that the idiosyncratic components of return are independent across stocks.
The topic Calculation of the Optimal Portfolio describes how the assumptions of the single-index model allow you to quickly calculate optimal portfolio weights.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System