![]() 7.10 RISK AVERSION AND THE MARKET PORTFOLIO
7.10 RISK AVERSION AND THE MARKET PORTFOLIO
Let the initial wealth at the beginning of the period be B, and let preferences be defined over the end-of-period wealth as discussed in the construction of an indifference map.
End-of-period wealth is fixed by the proportion of wealth invested in the market portfolio M times the 1 plus expected rate of return from M, plus the proportion of wealth invested in the risk-free asset times the one plus risk-free rate of return. Again let
ak be the fraction of investor k's wealth in the risk-free asset, and (1- ak) be the fraction in the market portfolio M. This is represented as follows:![]()
The investor's problem is to choose the share of the market portfolio,
ak, to maximize expected utility. Formally, this maximization problem is: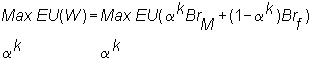
The first order condition for this problem is:
![]()
where the Uí is the derivative of U.
Suppose that the expected return on the market portfolio is greater than the risk-free rate of return and the optimal portfolio weight is
ak = 0. Evaluating the first order condition at this point will generate a contradiction between optimality and investing everything in the risk-free asset.This contradiction follows by observing that since W = Br
f and (rM - rf) > 0, the first order condition evaluated at this point is strictly positive. The utility function for a risk-averse investor is strictly concave and hence it is necessary and sufficient that the first order condition equal zero for the optimal portfolio.Therefore, it is never optimal to invest only in the risk-free asset when (E(r
M) - rf) > 0 and any expected utility maximizing risk-averse investor will allocate some part of their wealth to the market portfolio M.The interpretation of M as a value-weighted index forms the basis of the next topic, Empirical Tests of the CAPM.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System