![]() 3.9 Forward Contracts
3.9 Forward Contracts
A forward contract is an obligation to buy or sell an asset (real or financial) at a fixed time in the future and at a price that is agreed upon now. This price, called the delivery price, is paid at the time specified in the future, not at the time of entering into the forward contract. In fact, this security has the feature that no cash changes hands at the time the contract is made.
Because no cash is exchanged at the time of buying or selling, the arbitrage-free delivery price must be set so that the present value of the forward contract is zero. If this is not the case, then for a zero-cash outlay, either the buyer or the seller receives a positive net present value, which would violate the no-arbitrage requirement.
You can better appreciate the arbitrage implications by working through an example. Let:
![]()
![]()
Also, let f denote the forward price for a two period zero-coupon bond with face value F to be delivered at the end of Period 1:

The underlying bond is the two year zero coupon. At the time of delivery, it is a one period zero coupon. The current price of the zero-coupon bond is:
![]()
Arbitrage-Free Forward Price
Remember that, to prevent arbitrage, the forward price, f, must be set so that the net present value of settlement is zero. At the time of settlement, the buyer pays the forward price, f, in cash and receives the zero-coupon bond in exchange. Thus, at the end of Period 1, the forward price in cash is exchanged for a zero-coupon bond with one time period before its maturity date. For this forward price to be arbitrage-free, it should be equal to the value of the bond at this time.
Therefore, the value of the zero-coupon bond at the end of Period 1 is the face value, F, discounted by the Period 2 forward interest rate.
![]()
Therefore, the zero-arbitrage forward price equals:
![]()
That is, the forward price equals the present value of the underlying asset when viewed from the end of Period 1. To avoid creating an arbitrage opportunity, it must be that the appropriate interest rate is the one period forward rate that is implied from the current term structure.
Similarly, if viewed from the beginning of Period 1, to avoid creating an arbitrage opportunity, it must be that the present value of the forward price equals the price of the underlying zero-coupon bond.
Let us check that these arbitrage relationships do indeed hold. Suppose f exceeds the present value of the underlying zero-coupon bond at the end of Period 1 when we are using the forward interest rate as the interest rate. That is, suppose:
![]()
Now, assume you borrow the amount
![]()
for one period and use part of it to buy the two period zero-coupon bond and sell one forward contract. The price of the bond by assumption is strictly less than the amount borrowed, because from the definition of a forward interest rate, the price of the bond equals:
![]()
Therefore, with this transaction you have created a positive cash flow today.
At the end of Period 1, you receive f, deliver your zero-coupon bond, which has one period remaining, and pay back f. The net effect of this series of transactions is that you have completely closed out your position. Of course, you still have the cash left over from Period 1, so you have made an arbitrage profit.
If f is strictly less than
![]()
you would short sell the two period zero-coupon bond, invest the proceeds in the one period zero-coupon bond, and buy the forward contract. Again, this would generate an arbitrage gain because at the end of Period 1, you again close out your position, but this time by construction you have received more cash from the maturing one period zero-coupon bond than you are obligated to pay as the forward price f.
Because the market is unlikely to let you get away with such a profit (there is no free lunch), the forward price must indeed be as we calculated.
To make this a little less abstract, work through the following example.
Example: Bond Valuation using Forward Rates of Interest
Assume the three year term structure of spot interest rates is as follows:
|
Rate |
1+ Spot Rate |
|
0r1 |
1.0400 |
|
0r2 |
1.0696 |
|
0r3 |
1.0989 |
From the above spot rates you can compute the implied set of spot and forward rates as follows :
|
Rate |
Spot/Forward Rates |
|
0r1 |
0.04 |
|
1r2 |
0.10 |
|
2r3 |
0.16 |
The spot interest rates are 1.04, 1.0696, and 1.0989, respectiviely, and thus the present value of a two year zero-coupon bond using the spot rate is:
![]()
Equivalently, by using the spot and forward rates, the value of a two year zero-coupon bond is:
![]()
Now consider a forward contract that is defined on the two year zero-coupon bond, with settlement at the end of Year 1. What is the arbitrage-free forward price for this contract?
By applying the theory, you know that the forward price f is:
![]()
where F is $100 and the 1 + 1 year forward interest rate equals 1.10. As a result, the forward price, f, is $90.91.
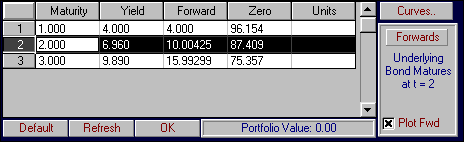
Online, click on the two year zero-coupon bond:
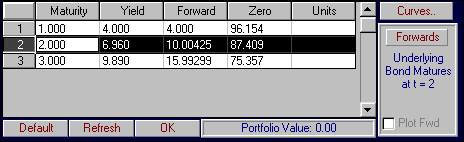
You can see that the present value of this bond is $87.409. By clicking on the Forward button, you will see the forward price of a forward contract defined on this two year zero and settled at the end of Year 1:
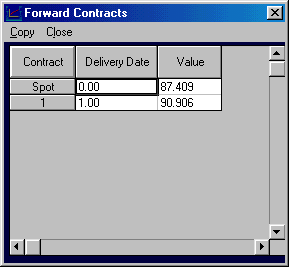
That is, the forward price equals $90.91. The Plot Fwd option now becomes active:
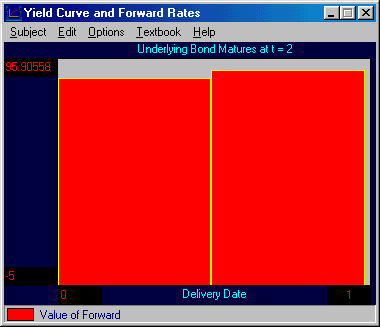
The Forwards contracts can be displayed graphically by clicking beside Plot Fwd as follows:
If this finding does not hold, there exists an arbitrage opportunity. Suppose that the forward price in the market is $92 per contract and that you can borrow or lend for one year at the 4% spot interest rate. How can you exploit this apparent price discrepancy?
Time: At the Beginning of Year 1
Continuing the above discussion, you can borrow $92/1.04 and buy one two year zero-coupon bond. That is, borrowing $88.46 and buying one two year zero-coupon bond at $87.41 leaves $1.05 per contract. In addition, you sell one forward contract at $92.
Suppose you engage in this transaction for 100,000 times the single unit case. This would leave +$105,000 left over at Time 0 because selling 100,000 forward contracts has no cash flow implications at Time 0 (the present).
Time: At the End of Year 1
At the end of Year 1, you reverse your position. The forward contract is settled and you receive per contract $92 in exchange for your long position in the two year zero (with only one year remaining). Your original loan of $92/1.04 is then settled for ($92/1.04) x 1.04 = $92. Therefore, this position is completely reversed except for the $1.05 per contract left over at the beginning of Year 1. You have thereby generated a riskless arbitrage profit.
Multi year Contract: Arbitrage-Free Forward Price
Consider a T period zero-coupon bond and a forward contract to deliver this bond in-period 2, so that the delivered bond will have (T-2) periods to maturity. Let P be the current price of the bond, and let f be the forward price.
You would like to argue that
![]()
so the forward price is the future value of the bond in-period 2, implied by the current term structure. The argument is complicated by the fact that if you try to adopt the strategy you followed in the one period case, you must be able to borrow for two periods at today's two period interest rate. This borrowed amount is:
![]()
That is, if you borrow this amount for two periods at the two period spot interest rate, (the interest rate that solves the following):
![]()
you can follow exactly the same strategy as before. That is, if f is greater than
![]()
you sell two period zero-coupon bonds to make the face value of these bonds in-period 2 equal to the forward price f , and use these proceeds to buy the T period bond at price P. Finally, you sell one forward contract.
In-period 2, you deliver the bond and receive f from the forward contract sold. Paying f to cover the two period bonds closes out the original two year bonds position.
By assumption,
![]()
So, you obtained more by selling the two period zero-coupons than you paid for the T period bond and thus generated an arbitrage profit. A reverse trading strategy would apply if the forward price is smaller than the future value of the T period bond at the time of settling the forward contract.
The Relationship between Spot Prices and Forward Prices
When there is a forward market, you have two alternatives for obtaining the underlying asset: (1) either purchase it directly now, or (2) purchase the forward contract now and take delivery of the asset at the time of maturity of the forward contract. Following the second alternative saves carrying the underlying asset from now until the maturity of the forward contract. As a result, the forward price is developed in terms of the future value of the underlying asset at the time of the forward contractís maturity.
In the market, however, it is the spot price of the underlying asset that is observable. The forward price in terms of the underlying spot price is:
![]()
The difference between the forward price and the spot price is often referred to as the carry cost, or, for interest rate contracts, the repo rate. For interest rate forwards, unlike commodity forwards, storage costs are presumably zero. Thus the "carry cost" or "repo rate" is the difference between the future value of the underlying asset and the present value of the underlying asset, which in the two period example is the two period spot interest rate:
![]()
We can provide an example of forward pricing by revisiting the three year example studied elsewhere in this chapter.
Example: Forward Prices
Let the three year term structure of spot interest rates be:
|
Rate |
1+ Spot Rate |
|
0r1 |
1.0400 |
|
0r2 |
1.0696 |
|
0r3 |
1.0989 |
From these spot rates, the implied set of spot and forward rates is :
|
Rate |
Spot/Forward Rates |
|
0r1 |
0.04 |
|
1r2 |
0.10 |
|
2r3 |
0.16 |
The present value of a three year zero-coupon bond using the spot rate is then:
![]()
The value of the two year zero-coupon bond is
![]()
Now, consider a forward contract that is defined on this two year zero-coupon bond that expires at the end of Year 1. What is the arbitrage-free forward price for this contract?
You have the choice of either working in terms of the face value of the underlying bond, F, or in terms of the current market price of the bond, P.
Taking the first approach, the forward price f is:
![]()
where F is $100 and the 1 + 1 year forward interest rate from Year 1 to Year 2 equals 1.10. As a result, the forward price, f, is $90.91.
Alternatively, the forward price can be viewed as the future value of the two year zero at the end of Year 1:
![]()
If this is not the case, then there is an arbitrage opportunity. Suppose that the forward price in the market is $92 per contract and that you can borrow or lend for one year at the 4% spot interest rate. How can you exploit this apparent price discrepancy?
Time: At the Beginning of Year 1
Continuing the above discussion, you can borrow $92/1.04 and buy one, two year zero-coupon bond. Borrowing $88.46 and buying one, two year zero-coupon bond at $87.41 leaves $1.05 per contract. In addition, you sell one forward contract at $92.
Time: At the End of Year 1
At the end of Year 1, you reverse your position. The forward contract is settled, and you receive per contract $92 in exchange for your long position in the two year zero (with only one year remaining). Your original loan of $92/1.04 is then settled for ($92/1.04) x 1.04 = $92. The position is completely closed except for the $1.05 per contract left over at the beginning of Year 1. As a result, you have earned a riskless arbitrage profit.
Online, you can see the relationship between spot and forward rates/prices by perturbing the current spot yield curve by clicking inside the small box and dragging it up or down.
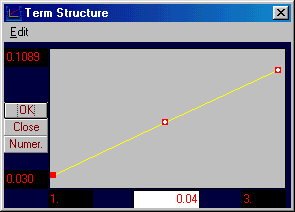
Click on the small solid box for Year 2 in the Yield Curve window. Holding the left mouse button, move this box down as follows:
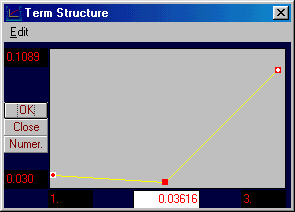
Click on OK and then the Numeric button. The current spot rates are provided numerically as follows:
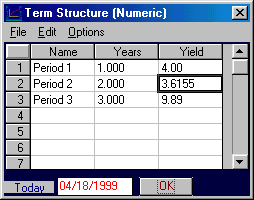
That is, the spot rate for Year 2 has been reduced to 3.6155%. The implication of this perturbation is displayed graphically in the forward-rate curve window.
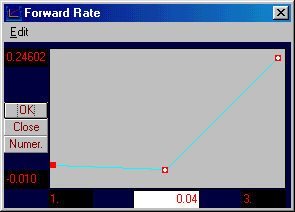
by clicking on the Numeric button:
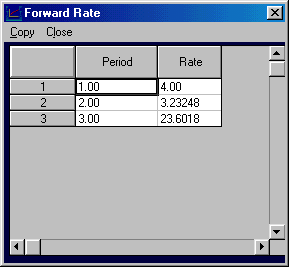
The effect of this perturbation in terms of values is provided in the main window (check that you turned Plot Fwd off (click beside the label to toggle on or off).
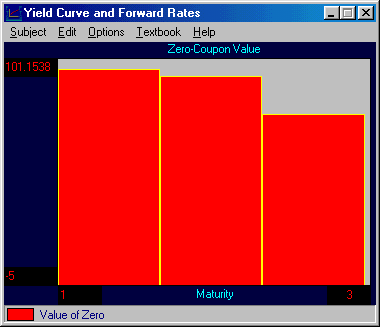
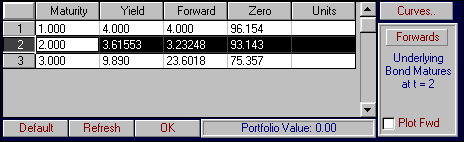
You can repeat this process by perturbing forward rates directly or for some portfolio of bonds where the units are entered under the Units column in the main window.
previous topic
next topic
(C) Copyright 1999, OS Financial Trading System