Trading Case RM1

Case Objective

This is a trading exercise designed to introduce traders to constructing synthetic fixed rate loans using forward rate agreements, interest rate caps and floors.

Key Concepts

Synthetic securities, international fixed income markets.

Case description

The Trarch Corporation borrowed $20,000,000 for 6-months for short term operations. Trarch considered two alternatives for borrowing this amount. Alternative 1, was to borrow the cash at the prevailing local fixed spot rate of 5% per annum. Alternative 2, was to borrow cash at the variable LIBOR (London Interbank Offered Rate) plus 50 basis points. Although Trarch’s management is very averse to interest rate fluctuations they chose the latter. They did this after discussing the loan with Trarch’s derivatives trader, Allan Thompson.

Allan Thompson, assured Trarch’s board that he could convert the variable rate Libor loan into a fixed rate loan that is approximately 75 basis points below the local fixed rate. Unfortunately shortly after proceeding with the loan Allan Thompson submitted his resignation to the board, to accept an overseas posting with a large Wall Street firm. As a result of this change the problem of converting the Libor loan into a fixed rate loan, fell into the hands of Christine Adams a recent MBA hire by Trarch.

Environment Overview

After gathering information on available FTS markets Christine identified the following set. A forward rate agreement market defined on a 45-day Eurodollar time deposit maturing at a specified point of time in the future. Interest rate cap and floor markets defined with respect to the 90-day spot Libor and paid every 3-months.

With respect to these markets her analysis reveals that the current 45-day spot LIBOR rate is 3.75% and at the beginning of subsequent 45-day periods analysts expect that the set of possible spot LIBOR realizations is as indicated below.

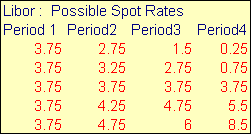
Each period’s realization for the Libor spot rate is independent.

Realized interest on Trarch’s variable loan is paid at the end of each period applying the current period’s spot rate. That is, at the end of period 1 the interest expense is known to be 20,000,000 * (0.0375 + margin) * 45/360 = $100,625 when the margin is 50 basis points. Subsequent to period 1, however, the interest expense depends upon the realized spot LIBOR rate in accordance with the above table. The day count for each period is always applied as 45/360.

Key Facts

In this case you can buy and sell securities 3-6 (as described below) at the given prices. Your objective is to convert your variable rate loan into a fixed rate loan. That is, you would like to ensure that your net interest payments each period, net of any derivatives added to your loan position, is constant. This is equivalent to converting a variable rate loan into a “synthetic” fixed rate loan.

The following additional market conventions apply to this trading exercise.

Fts markets

Security 1: loan contract

Security 1 is a unit LIBOR loan (original deposit $80,000). Trarch has borrowed $20,000,000 which is represented as 250 units short in security 1. Interest is payable every 45 days at the spot rate plus 50 basis points. There are four interest payment dates: at the end of period 1, period 2, period 3, and period 4.

Example: Suppose the realized spot rate for period 3 is 4.75%. Interest expense at the end of period 3 equals (0.0475+0.005)*20,000,000*45/360 = 131250 or 525 per 80,000 unit.

Security 2: Interest On A 45-Day Eurodollar Time Deposit

This security is a claim to the interest on a $80,000 45-day Eurodollar time deposit maturing at the end of period 3. In the FTS markets you can only trade a forward rate agreement defined on this deposit’s interest. That is, the notional principal is $80,000 and settlement is in cash.

Example: Security 2

Suppose the realized period 3 spot rate is 2.75%. The terminal deposit value of the 45-day Eurodollar deposit is $80,000 * (1 + 0.0275 * 45/360) = $80,275. As a result, the interest revenue is $275.

Security 3: Libor Index

This is a non tradable index used to settle 3-month interest rate caps and floors. The index is determined from the realized interest using realized spot 3-month Libor times the notional principal amount of $80,000 (day-count 90/360). You can assume that the LIBOR index is computed in the following manner. For period 2 suppose 3.25% is the spot realized LIBOR rate. Assume that row 2 period 2 for the index is computed from the sum of this 45-day rate plus 3.75 applied for 45-days. That is, 80,000*(0.0325*45/360+0.0375*45/360) = 700.

Similarly, for period 4 the simplifying assumption is that it is the sum of 0.0375 plus the period 4 realized rate applied in the same way as before.

Note: The index has been constructed under a simplifying assumption using the sum of the two 45-day spot rates as opposed to the product of 1+ 45-day spot rates. This simplifies payoffs in the case to as provided in the table below.

Security 4: Forward Rate Agreement Contract

A forward rate agreement contract is defined upon the realized interest from security 2 (45-Day Eurodollar time deposit). In practice these agreements are settled at the beginning of the maturity period for the present value taken with respect to the time to maturity of the underlying LIBOR deposit. The reason for this real world convention is because the spot rate is realized at the beginning of the period but interest accrues over the period. By applying this timing/present value convention retains the relevance of a FRA for hedging LIBOR risk.

In the FTS market this convention will be applied with the following additional adjustment. In this trading case you can only trade periods 1 and 2. That is, you must set up all hedges by the end of the second trading period. After period 2 closes your position is automatically marked at the end of periods 3 and 4 given the realized LIBOR spot rates. As a result, the (positive or negative) proceeds from the FRA are automatically invested for period 3 at the realized spot 45-day LIBOR rate. These two steps are illustrated by example below:

Example:

Step 1: Suppose the realized period 3 spot rate is 2.75%. The interest on the 45-day Eurodollar deposit is $80,000 * (0.0275 * 45/360) = $275. If you are long 1 FRA this is settled at the beginning of period 3 as follows:

($275 - FRA price)/(1+0.0275*45/360)

Step 2: At the end of period 3 your position is marked as follows:

(($275 - FRA price)/(1+0.0275*45/360) )* (1+0.0275*45/360)

The net effect of these two steps is that your position is marked at the end of period 3 per long FRA contract as:

($275 - FRA price)

and if you are short FRA’s then your position is marked as:

(FRA price - $275)

That is, you earn the difference between the realized interest on security 2 and the price you paid for the FRA.

In this trading case the prices for the FRA are determined outside of the FTS markets. You can buy or sell any number of FRA’s at the prevailing market price which is determined outside of the FTS markets.

Security 5: Interest Rate Cap

The interest rate cap is a hybrid form of a European option. For an up front fee (the option premium) a buyer of the cap at the end of each 3-month period receives from the cap writer the maximum of 0 and the difference between the LIBOR index (security 3 above) and the strike rate times the principal. The strike rate is 750 relative to the $80,000 notional. As a result, if 850 is the realized rate at the end of period 2 (i.e., row 5 period 2 in the LIBOR index table above), the cap buyer receives from the writer the net difference 100 per contract. However, a cap provides a sequence of payments unlike a regular call option. In this case there are two “caplets” that make up one cap. That is being long one unit of a cap implies that you are long one unit of each caplet. Each caplet has a strike price of 750 but a different time of maturity. But each caplet can finish in the money. That is, at the end of period 2 and at the end of period 4 you can receive cash from a cap because each of the two “caplets” mature at different points in time (end of period 2 and 4 respectively). The possible payoffs from a long position of 1 cap are:

In this trading case the prices for caps are determined outside of the FTS markets. These prices are well approximated by Blacks model for valuing caps and floors. You can buy or sell any number of caps at the prevailing market price which is determined outside of the FTS markets.

Security 6: Interest Rate Floor

The interest rate floor is a hybrid form of a European option. For an up front fee (the option premium) a buyer of the floor at the end of each 3-month period receives from the floor writer the maximum of 0 and the difference between the strike rate and the LIBOR index (security 3 above) times the principal. The strike rate is 750 relative to the $80,000 notional. Suppose 850 is realized at the end of period 2, the floor buyer receives from the writer 0 because the closing realization is higher than the strike price.

The floor pays off at the end of period 2 and at the end of period 4. The possible payoffs from a long position of 1 floor are:

In this trading case the prices for caps are determined outside of the FTS markets. These prices are well approximated by Blacks model for valuing caps and floors. You can buy or sell any number of floors at the prevailing market price which is determined outside of the FTS markets.

Time Line For The Variable Rate Loan (Security 1)

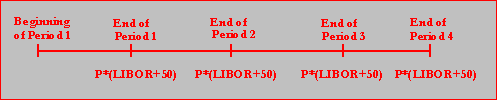
Time line for the interest on a 45-day eurodollar deposit

(security 2)

Time Line For The Libor Index (Security 3)

Time Line For The Forward Rate Agreement (Security 4)

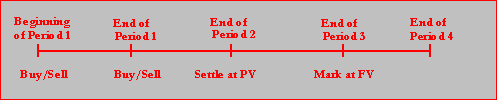
Time Line For The Interest Rate Cap (Security 5)

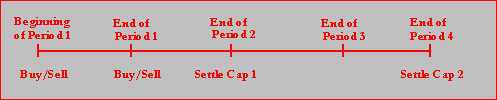
Time Line For The Interest Rate Floor (Security 6)

The Trading Objective

As a trader for Trarch you job is to manage interest payment cash flows. To complete this task you can trade in periods 1 and 2 only. That is, you must set up your position in the first two periods even though your position will be marked to market at the end of each of the four periods.

Your initial cash budget is the present value of receiving $200,000 at the beginning of each period discounted back at the expected LIBOR rate 3.75. At the end of each period the aggregate of the realized interest expense plus payoffs from any derivative securities are deducted/added to this initial balance. In order to manage the cash flows your trading objective is to keep this aggregate of interest expense and derivative payoffs constant at the end of each period. This is because by so doing you have created fixed interest payments from your synthetic fixed rate loan.

That is if Trarch had entered into a 5% fixed rate loan, the closing cash balance would be the present value of the $200,000 cash annuity paid in advance less the constant interest expense that you can engineer by exploiting the derivative markets. Your trading objective is to beat $125,000 fixed interest expense that would accrue if you enter into a 5% fixed rate loan. Ideally, you want to attain Allan Thompson’s original prediction to the board of lowering the borrowing costs by approximately 75 basis points.

Earning Grade Cash

At the end of the trial you will earn grade cash based upon how well you have managed to control your interest expense cash flows. If at the end of the trial you have a closing balance of $275,000 or higher (up to 1,000,000) you will earn grade cash as follows up to maximum of $10 per period:

If your closing balance falls below $275,000 in any period you lose $10 each time.

Trading is conducted over a number of independent trials and a record of your cumulative grade cash is maintained.