FTS Treasury Calculator:  Cubic Spline and Nelson-Siegel Approaches

Yield curves cannot be directly observed, instead they can only be inferred from market prices.  As a result, when estimating a yield curve in practice one attempts to estimate a smooth curve from a relatively small number of fixed income prices.  The cubic spline approximation to a yield curve smooths out the interior bumps by matching both slope and curvature at each interior yield to maturity node that is inferred from some market price.  An immediate problem that arises is how to handle the beginning and end points in the data set.  The natural cubic spline sets the slope at the endpoints to zero.  This is default case in the Treasury Calculator module.    Alternatively, the module lets you experiment with "clamping" by setting the slope at the endpoints to being non zero constants.  This sets the second derivatives to equal zero.  However, usually the reason for using a spline in the first place is to come up with a smooth curve that requires minimal complexity --- this is provided by the "natural cubic spline" a third order polynomial equation with the slopes at each endpoint set to equal zero.

The Nelson-Siegel analytic approximation (see Journal of Business Vol 60, Issue 4, October 1987)  requires estimating three parameters, beta 0, 1 and 2 below.  The module lets you estimate the best fit to the observed (non smoothed curve) and then adjust the three parameters by visually smoothing the fitted curve.  You can use the +/- button to adjust the level, slope and curve numbers.  To control each number first click onside the text box that you want to change and then click on either +/-.  You can see the impact of the change by observing the display window.  In their original paper the authors claim to explain 96% of T-bill yields between 1981 to 1983 (a volatile period of time).

In the following equation, r(t) is the yield to maturity for maturity t, tau is a time constant associated with the equation and the betas are the three constants of the equation given by the initial conditions.  Their fitted equation in the Treasury Calculator module has the following form (where tau is treated as a constant to avoid over-identification and is set to equal 3):

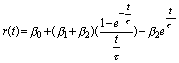
OS Financial Trading System, PO Box 11356, Pittsburgh, PA 15238 USA, Phone 1-800-967-9897, Fax 1-412-967-5958, Email fts@ftsweb.com,