![]() Replicating
a Call Option in the Binomial Model
Replicating
a Call Option in the Binomial Model
Exercise:
Using the default data set in Option
Tutorís Binomial Replication subject, explain carefully how you can replicate a
two-period call option synthetically. You should
describe exactly what trades are required over the two periods.
To
conduct this exercise, launch the Binomial Tree Module from the Virtual
Classroom:
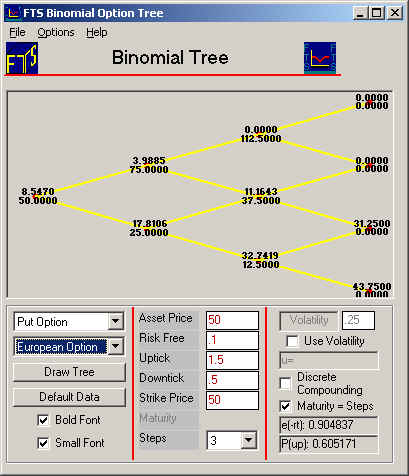
On the Action part of the Window, select 2 from the drop down beside Steps and select Call from the drop down on the left side of the screen. We will also illustrate this for discrete compounding and check that Maturity = Steps. This means that the time to maturity for this option equals the number of steps (i.e., 2-periods). The screen should appear as depicted below. Be careful to check beside Discrete Compounding as displayed below.
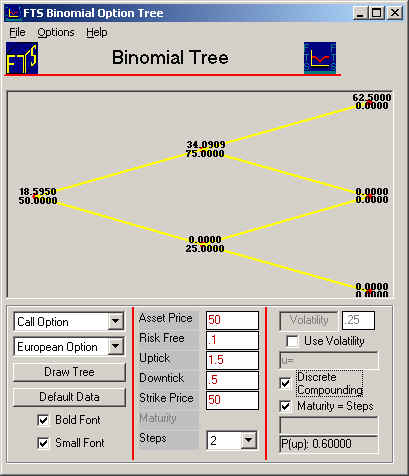
You
can see all the nodes of the 2-period binomial tree.
The current node is highlighted in blue, and the call option price at the
current node is $18.595. The
stock price at this node is 50, as shown in the Action Window. When there
is an uptick, the stock price moves to 75 (1.5 times 50) and similarly 25 for
the downtick (0.5 times 50).
You
can see that the stock price at this node is 75, while the call option price is
$34.091.
Next select Call Replication from the drop down as depicted below:
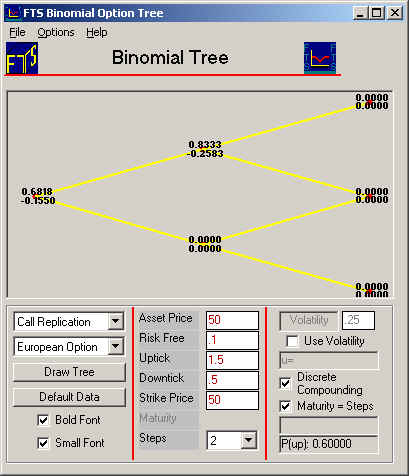
Notice the tree depicts weights now. The top weight refers to the number of stocks and the bottom weight in each pair the number of bonds, required to replicate one call option. By tracking how these numbers change we can formulate a trading strategy that creates a position that exactly mimics a call option. To see why consider the following, initially by working backwards from the terminal nodes:
Beginning of Period 2:
Consider the top middle node above, long 0.8333 stocks and short 0.2583 pure discount bonds with a face value equal to 100*1.1^2. The terminal payoff from this is either:
112.5*0.8333 - 0.2583*121 if an up tick is realized in period 2, or
37.5*0.8333 - 0.2583*121 if a down tick is realized
Respectively this is: 62.5 if an up-tick and 0 if a down tick is realized.
The node below this is 0, 0 because irrespective of the tick the call option finishes out of the money if this node is reached.
Beginning of Period 1:
From the Tree that depicts the Call option (see below):
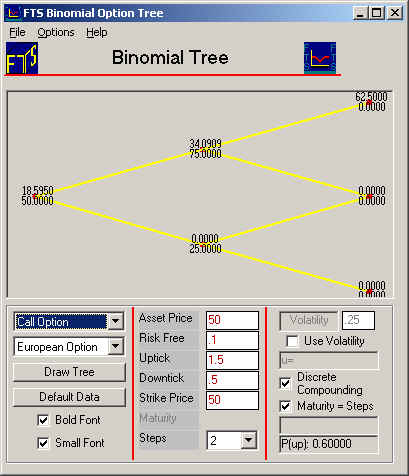
Observe that at the beginning of period 1 the two possible end of period values for the call option are: 34.0909 and 0 depending upon whether an up or down tick is realized for the underlying.
As a result, again we need to identify the replicating portfolio of stocks and bonds that can mimic this payoff.
The call replication tree (two screens above) reveals that the weights are:
0.6816 Stocks, and -0.1550 Bonds.
To check this observe that: 0.6816*75 - 0.1550*100*1.10 = 34.09 and 0.0 respectively for an up or down tick.
So by working backwards we can identify the appropriate position weights that mimic the call option. But observe that these weights change from node to node. This implies that to implement this solution we can only work forward in time. As a result, need to rebalance our position as we move forward through the tree. That is, we can only mimic the option values by a trading solution!
Trading Solution
Now we need to keep track of the
starting and ending
portfolio weights so we can identify the appropriate trades. When you replicate an
option by trading, you must trade stocks and bonds in at the first node to
obtain the same values as the call at the two nodes in period 1.
The difference between the start and end position at a node is the net
trade at the node. If you keep
track of all the net trades, then as you work through the tree, you define what
is called a trading strategy.
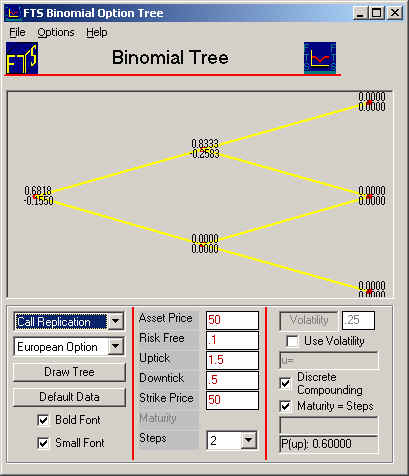
Refer to the call replication tree depicted above. This contains position weights relative to 1 unit of the stock. Therefore, if you start period 1 with 0.6818 stocks and an up tick is realized then you want to start period 2 with 0.8333 stocks. To do this requires that you buy 0.8333 - 0.6818 = 0.1515 stocks and sell an additional (.2583 - 0.1550) bonds upon reaching this node.
Similarly, if a down tick was realized you want to start period 2 with 0 stocks and 0 bonds. This implies that you will sell 0.6818 stocks and buy back 0.1550 bonds contingent upon a down tick being realized for period 1.
To
summarize, the trading strategy required to replicate the call is:
Period
1: Buy 0.6818 stocks, sell 0.1550 bonds.
If
there is a downtick, sell 0.6818 stocks, buy 0.1550 bonds, leading to zero
stocks and zero bonds.
In
an up tick, buy an additional 0.1515 stocks and sell 0.125 bonds, leading to
+0.8333 stocks and -.2583 bonds.
The
stock and bond portfolio will now track the call options payoffs.
In the next lesson we will consider how we can exploit these trading principles to manage risk.
(C) Copyright 2003, OS Financial Trading System