![]() Example 3: European and American Options
Example 3: European and American Options
Exercise:
In a three-period binomial world, explain
the difference between the values of European and American options.
To conduct
this exercise, select the “Binomial Tree” module from the Virtual Classroom:
You will
see a three-period binomial tree displayed with the following Action and
Display Screen.
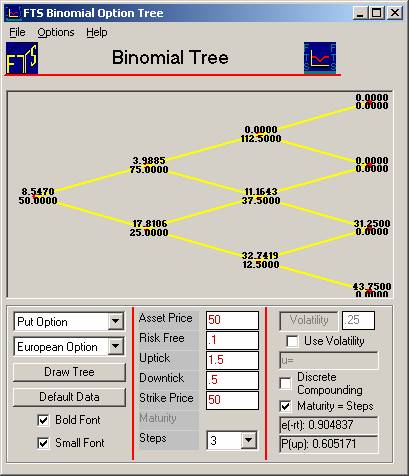
The tree
displayed is that of the underlying asset, which in this problem we will
interpret as a stock. You can see that
the stock price is initially 50, and then moves to either 75 or down to 25, and
so on. The default values have the
strike price also at 50, so the options are “at the money.”
Let us
look at the trees for European and American put options using the default
parameters. The above screen has the
default provided for the European Option (see drop down above). Below we depict the equivalent screen for the
American put option by changing the drop down to American.
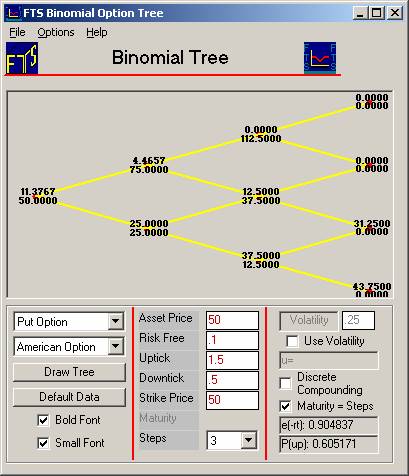
You can
see that the European put is valued at 8.547 while the American put is worth
11.377. Comparing the trees, you can see
that they differ along the bottom-most path.
After two downticks, the European put is worth 32.742 while the American
put is worth 37.50. At this node, the
stock price is 12.5, so the intrinsic value of the put is 37.50. The numbers in the tree show you that if you
do not exercise the put, it is worth 32.742 while if you exercise it, it is worth
37.50. Consequently, it is “rational” to exercise the put before maturity.
Let us
verify this by calculating the value of the put if you did not exercise. In the next period, the put would be worth
either 43.75 (if there was a further downtick) or 31.25 (if there was a
subsequent uptick).
The risk neutral probability is given by the formula: ![]()
Here, r is
1 plus the risk free interest rate, u is the uptick
parameter and d is the downtick parameter.
For our values, r = ![]() ,
u = 2, and d = .5. This implies that p =
0.605171 (as shown in the action window).
Using the principle of risk-neutral valuation, we find that the value of
the put option at the node is:
,
u = 2, and d = .5. This implies that p =
0.605171 (as shown in the action window).
Using the principle of risk-neutral valuation, we find that the value of
the put option at the node is:
![]()
Therefore,
the difference between the European and American option values is caused by the
fact that after two downticks, you would exercise the American style option.
©2003
OS Financial Trading System